3.6 稀疏向量算法：高于阈值算法

我们首先论证了 AboveThreshold 算法是私有的，并且是准确的，该算法专门针对一个高于阈值的查询。

（注：上面算法中 $\bot$ 为永假含义; $\top$ 为永真含义。根据上章节描述，个人理解其含义应为：$\top$ 释放回答，$\bot$ 拒绝回答）

定理 3.23 AboveThreshold 算法是 $(\varepsilon,0)$- 差分隐私的。

【证明】 固定任意两个相邻数据库 $D$ 和 $D'$。设 $A$ 为表示 AboveThreshold算法 $(D,{f_i},T,\varepsilon)$ 输出的随机变量，设 $A'$ 为表示 AboveThreshold算法 $(D',{f_i},T,\varepsilon)$ 输出的随机变量。算法的输出是这些随机变量的一些实现，即：$a \in \{\bot,\top\}^k$，其形式是对于所有的 $i<k,a_i=\bot,a_k=\top$ 。算法内部有两种类型的随机变量：噪声阈值 $\hat{T}$ 和对 $k$ 个查询的扰动 $\{\nu_i\}_{i=1}^k$。在下面的分析中，我们将固定（任意的）$\nu_1,...,\nu_{k-1}$ 的值。并且 $\nu_k$ 和 $\hat{T}$ 具有随机性。定义以下量，该量代表在 $D$ 上估计任何查询 $f_1,...,f_{k-1}$ 的最大噪声值：

$g(D) = \max_{i<k}(f_i(D) + \nu_i)$

在下文中，我们将滥用表示法，将 $\text{Pr}[\hat{T}=t]$ 写为 $\hat{T}$ 在 $t$ 处的概率密度函数的简写（$\nu_k$ 也类似这样的表示），并写 $\mathbf{1}[x]$ 表示事件 $x$ 的指示函数$\ ^{<1>}$。注意固定 $\nu_i,...,\nu_{k-1}$ 的值（这使 $g(D)$ 为确定量），我们有：

$\begin{aligned} \underset{\hat{T},\nu_k}{\text{Pr}}[A=a] &= \underset{\hat{T}, \nu_k}{\text{Pr}}[\hat{T} > g(D) \ \text{and} \ f_k(D)+ \nu_k > \hat{T}]\\ &= \underset{\hat{T}, \nu_k}{\text{Pr}}[\hat{T} \in (g(D),f_k(D)+ \nu_k]]\\ &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\text{Pr}[ \nu_k=v]\\ &\ \enspace \ \cdot \text{Pr}[\hat{T}=t]\mathbf{1}[t\in (g(D),f_k(D)+v]]dvdt\\ &= * \end{aligned}$

我们现在对变量做一些变换，定义：

$\begin{aligned} \hat{v} &= v+g(D)-g(D')+f_k(D)-f_k(D')\\ \hat{t} &= t + g(D) - g(D') \end{aligned}$

注意，对于任何 $D,D'$，有 $|\hat{v}-v|\leq 2,|\hat{t}-t|\leq 1$ 。这是因为每个查询 $f_i(D)$ 的敏感度都是 $1$ 的，因此量 $g(D)$ 的敏感度也是 $1$ 。应用变量的这种变化，我们有：

$\begin{aligned} * &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\text{Pr}[\nu_k=\hat{v}]\cdot\text{Pr}[\hat{T}=\hat{t}]\mathbf{1}[(t+g(D)-g(D'))\\ &\ \qquad \qquad \enspace \in(g(D),f_k(D')+v+g(D)-g(D']]dvdt\\ &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\text{Pr}[\nu_k=\hat{v}]\cdot\text{Pr}[\hat{T}=\hat{t}]\mathbf{1}[t\in(g(D'),f_k(D')+v]]dvdt\\ & \leq \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\exp(\varepsilon/2)\text{Pr}[\nu_k=v]\\ &\enspace \enspace \cdot \exp(\varepsilon/2)\text{Pr}[\hat{T}=t]\mathbf{1}[t\in(g(D'),f_k(D')+v]]dvdt\\ &= \exp(\varepsilon)\underset{\hat{T},\nu_k}{\text{Pr}}[\hat{T} > g(D') \ \text{and} \ f_k(D')+ \nu_k > \hat{T}]\\ &= \exp(\varepsilon)\underset{\hat{T},\nu_k}{\text{Pr}}[A'=a] \end{aligned}$

不等式来自 $|\hat{v}-v|$ 和 $|\hat{t}-t|$的界，以及 Laplace 分布的概率密度函数。

【定理 3.23 证毕】

【补充：对上述证明过程中的不等式步骤拓展解释。由 Laplace 分布概率密度函数（ $v$ 的尺度参数为 $4/\varepsilon$）可知：

$\begin{aligned} \text{Pr}[\nu_k = \hat{v}] &= \frac{1}{2\cdot\frac{4}{\varepsilon}}\exp\big(-\frac{|\hat{v}|}{4/\varepsilon}\big)\\ \text{Pr}[\nu_k = v] &= \frac{1}{2\cdot\frac{4}{\varepsilon}}\exp\big(-\frac{|v|}{4/\varepsilon}\big)\\ \end{aligned}$

由于 $|\hat{v}-v|\leq 2$，并且由绝对值不等式，可以作出如下推导：

$\begin{aligned} \frac{\text{Pr}[\nu_k = \hat{v}]}{\text{Pr}[\nu_k = v]} &= \exp\bigg(\frac{|v|-|\hat{v}|}{\frac{4}{\varepsilon}}\bigg)\\ &\leq \exp\bigg(\frac{|v-\hat{v}|}{\frac{4}{\varepsilon}}\bigg)\\ &\leq \exp\bigg(\frac{2}{\frac{4}{\varepsilon}}\bigg)\\ &= \exp\big(\frac{\varepsilon}{2}\big)\\ \implies \text{Pr}[\nu_k = \hat{v}] &\leq \exp\big(\frac{\varepsilon}{2}\big)\cdot \text{Pr}[\nu_k = v] \end{aligned}$

同样的方法应用于 $\hat{T}$ 上，其 Laplace 分布的尺度参数为 $2/\varepsilon$，且 $|\hat{t}-t|\leq 1$

】

（译者注<1> 指示函数：是定义在某集合 $X$ 上的函数，表示其中有哪些元素属于某一子集 $A$。集合 $X$ 的子集 $A$ 的指示函数是函数 $\mathbf{1}_{A}:X\to \lbrace 0,1\rbrace$，定义为：

$\mathbf{1} _{A}(x)= \begin{cases} 1 &\text{if}\enspace x \in A,\\ 0 &\text{if}\enspace x \notin A. \end{cases}$

详见：指示函数定义 ）

定义3.9（准确度） 一个算法它的应答流 $a_1,...,\in \{\top,\bot\}^{*}$ 作为对 $k$ 个查询流 $f_1,...,f_k$ 的响应。如果除了概率最大为 $\beta$ 之外，这个算法在 $f_k$ 之前不停止，并且对于所有 $a_i = \top$ 有： $f_i(D) \geq T - \alpha$ 对于所有 $a_i = \bot$ 有： $f_i(D) \leq T + \alpha$ 那么，我们称这个算法对于阈值 $T$ 是 $(\alpha,\beta)$ -准确的。

算法1 可能出什么问题？噪声阈值 $\hat{T}$ 可能离 $T$ 很远，例如 $|\hat{T}-T|\geq \alpha$。 另外，小的 $f_i(D)<T-\alpha$ 可能会添加大量噪声，以至于报告为高于阈值（即使阈值接近正确），而大 $f_i(D)>T+\alpha$ 可能报告为低于阈值。所有这些都以 $\alpha$ 的指数形式发生，概率很小。总而言之，我们在选择噪声阈值时可能会遇到问题，或者在一个或多个单独的噪声值 $ν_i$ 中可能会遇到这种问题。当然，我们可能同时存在两种错误。因此在下面的分析中，我们为每种类型分配 $\alpha/2$。

（个人理解：AboveThreshold 中需要向阈值 $T$ 和扰动 $\nu_k$ 添加 Laplace 噪声。根据 Laplace 分布的特点（下图）：

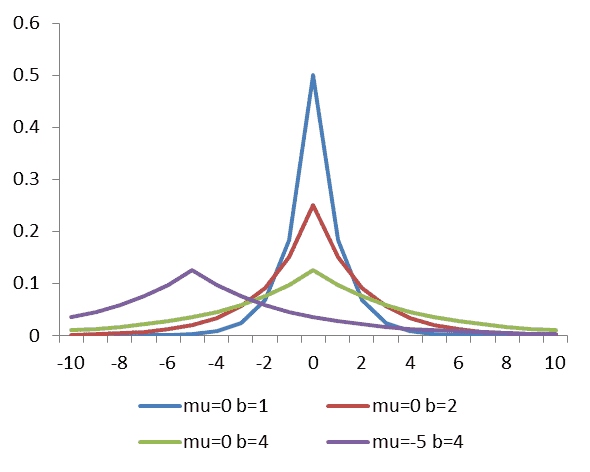
可以看出，算法会以小概率对阈值和扰动添加过大的噪声。如图的左右两侧。这就会造成上文提到的 “噪声阈值 $\hat{T}$ 可能离 $T$ 很远，例如 $|\hat{T}-T|\geq \alpha$”。同样，对扰动的噪声也可能过大。这样就导致，即使 $\hat{T}$ 与 $T$ 接近的情况下，造成小值回答（不允许释放）超过阈值被释放；大值回答（允许释放）小于阈值被拒绝。由于 AboveThreshold 会出现这两种错误，进而不满足 定义3.9 的规定。所以对于这两种错误情况，下面定理为噪声阈值 $\hat{T}$ 和 扰动 $\nu_k$ 各分配 $\alpha/2$ 的界。并将概率上界 $\beta$ 和噪声取之范围 $\alpha$ 关联起来，使得 AboveThreshold 算法不会出现两种错误情况，进而满足 定义3.9 的规定。 ）

定理 3.24 对于 $k$ 个查询的任何序列，$f_1,...,f_k$ 使得 $|\{i<k:f_i(D)\geq T - \alpha\}|=0$（即，唯一接近阈值以上的查询是最后一个），当：

$\alpha = \frac{8(\log k+\log(2/\beta))}{\varepsilon}$

AboveThreshold 算法 $(D,{f_i},T,\varepsilon)$ 是 $(\alpha,\beta)$-准确的：

【证明】 如果我们能够证明除概率最大为 $\beta$ 以外，当:

$\max_{i \in [k]}|\nu_i|+|T-\hat{T}|\leq\alpha \qquad (*)$

时，由观察易得该定理。

如果是这样的情况，那么对于任意 $a_i=\top$，有：

$f_i(D) + \nu_i \geq \hat{T} \geq T-|T-\hat{T}| \qquad (1)$

进一步推导：

$f_i(D) \geq T-|T-\hat{T}|-|\nu_i|\geq T-\alpha \qquad (2)$

同样的，对于任意 $a_i = \bot$，有：

$f_i(D) \leq \hat{T} \leq T+|T-\hat{T}|+|\nu_i|\leq T+\alpha$

我们将会有对于任意 $i<k:f_i(D)<T-\alpha<T-|\nu_i|-|T-\hat{T}|$。所以： $f_i(D)+\nu_i\leq \hat{T}$，即：$a_i=\bot$。因此，算法在第 k 个查询被回答前不会停止。

我们现在完成证明。回忆一下 事实3.7，当 $Y\backsim Lap(b)$ 时，$\text{Pr}[|Y|\geq t\cdot b]=\exp(-t)$，算法中 $\hat{T}$ 的尺度参数 $b=2/\varepsilon$ 因此我们有：

$\text{Pr}[|T-\hat{T}|\geq \frac{\alpha}{2}]=\exp\Big(-\frac{\varepsilon \alpha}{4}\Big)$

由定理设定最大概率为 $\beta/2$，我们可以得知：$\alpha\geq \frac{4\log(2/\beta)}{\varepsilon}$ 。

同样，由 布尔不等式，且算法中 $\nu_k$ 的尺度参数 $b=4/\varepsilon$可知：

$\text{Pr}[\max_{i\in [k]}|\nu_i|\geq \alpha/2]\leq k\cdot\exp\Big(-\frac{\varepsilon \alpha}{8}\Big)$

由定理设定最大概率为 $\beta/2$，我们可以得知：$\alpha\geq \frac{4\log(2/\beta)+\log k}{\varepsilon}$ 。

这两个推导共同证明了该定理。

【定理 3.24 证毕】

【补充(1)式：在 AboveThreshold 算法中，当 $a_i=\top,f_i(D)+\nu_i\geq \hat{T}$，$|T-\hat{T}|$ 为 Laplace 噪声，故阈值必然大于等于其下界 $T-|T-\hat{T}|$ 】

【补充(2)式：由 $(*)$ 可以推得：

$\begin{aligned} \max_{i \in [k]}|\nu_i|+|T-\hat{T}|&\leq\alpha\\ \implies |\nu_i|+|T-\hat{T}| &\leq \max_{i \in [k]}|\nu_i|+|T-\hat{T}| \leq \alpha\\ \implies -|\nu_i|-|T-\hat{T}| &\geq -\alpha\\ \implies T-|\nu_i|-|T-\hat{T}| &\geq T-\alpha \end{aligned}$

】